|
- Математик.
- Жил приблизительно в середине II или III в. до н.э. Прожил 84 года.
- До наших дней дошли два произведения, но оба не полностью.
- "АРИФМЕТИКА" (6 книг из 13) - стала поворотным пунктом в развитии алгебры и теории чисел.
- Отрывки из трактата "О МНОГОУГОЛЬНЫХ ЧИСЛАХ".
- Труды Диофанта имели фундаментальное значение для развития алгебры и теории чисел.
- С его именем связано появление и развитие алгебраической геометрии.
|
ПРАВИЛО ЗНАКОВ
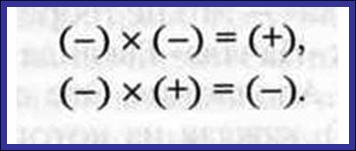
Диофант пишет:
"Недостаток, умноженный на недостаток, дает наличие; недостаток же, умноженный на наличие, дает недостаток".
|
- О подробностях его жизни практически ничего неизвестно. С одной стороны, Диофант цитирует Гипсикла (II век до н. э.); с другой стороны, о Диофанте пишет Теон Александрийский (около 350 до н.э.), откуда можно сделать вывод, что его жизнь протекала в границах этого периода.
- Возможное уточнение времени жизни Диофанта основано на том, что его "АРИФМЕТИКА" посвящена "достопочтеннейшему Дионисию". Полагают, что этот Дионисий - не кто иной, как епископ Дионисий Александрийский, живший в середине III в. до н. э.
- В Палатинской антологии содержится эпиграмма - задача, из которой можно сделать вывод, что Диофант прожил 84 года:
 
- В X веке "АРИФМЕТИКА" была переведена на арабский язык, после чего математики стран ислама (Абу Камил и др.) продолжили некоторые исследования Диофанта.
- В Европе интерес к "АРИФМЕТИКЕ" возрос после того, как Рафаэль Бомбелли обнаружил это сочинение в Ватиканской библиотеке и опубликовал 143 задачи в своей "АЛГЕБРЕ" (1572 г.).
- В 1621 году появился классический, подробно прокомментированный латинский перевод "АРИФМЕТИКИ", выполненный Баше де Мезириаком.
 
- Методы Диофанта оказали огромное влияние на Франсуа Виета и Пьера Ферма.
- В XX веке под именем Диофанта обнаружен арабский текст еще 4 книг "АРИФМЕТИКИ". Проанализировав этот текст И. Г. Башмакова и Е.И. Славутин выдвинули гипотезу, что их автором был не Диофант, а хорошо разбиравшийся в методах Диофанта комментатор, вероятнее всего - Гипатия.
- Трактат Диофанта "О МНОГОУГОЛЬНЫХ ЧИСЛАХ" сохранился не полностью; в сохранившейся части методами геометрической алгебры выводится ряд вспомогательных теорем.
- Из сочинения Диофанта "ОБ ИЗМЕРЕНИИ ПОВЕРХНОСТЕЙ" и сочинения "ОБ УМНОЖЕНИИ" также сохранились лишь отрывки.
- Книга Диофанта "ПОРИЗМЫ" известна только по нескольким теоремам, используемым в "АРИФМЕТИКЕ".
|
на главную страницу
|